2.1. Decision Tree (의사결정 나무)

본 포스팅은 충남대학교 박정희 교수님의 기계학습 수업과 으뜸 머신러닝 (강영민 , 박동규 저)를 참고하였습니다.
 
 

결정 트리를 이용한 분류

결정 트리는 decision tree라고도 합니다. 결정 트리는 귀납 추론을 위해 자주 사용되는 실용적인 방법입니다.
일반적인 트리 구조를 생각 해보면 가장 위에 루트 노드(root)에서 시작하여 차례로 중간 노드(internal)들을 거쳐 단말 노드(leaf)로 마무리 되는 구조입니다.
결정 트리도 일반적인 트리 구조를 따라 루트 -> 중간 -> 단말 순으로 알고리즘을 실행합니다.
이렇게 순차적으로 내려가는 방식을 rule - base라고 합니다.

그림을 살펴보면 '공의 크기' 부분이 가장 위에 있으므로 루트 노드입니다.
'경기장 중앙 네트', '손을 쓰냐' 부분은 중간 노드가 되고 나머지 '야구', '축구', '농구', '배구'는 단말 노드에 속합니다.
Decision tree는 결국 root node와 internal node에서 데이터를 알맞게 분류한 후, 클래스들을 leaf node로 분류하는 알고리즘을 말합니다.
 

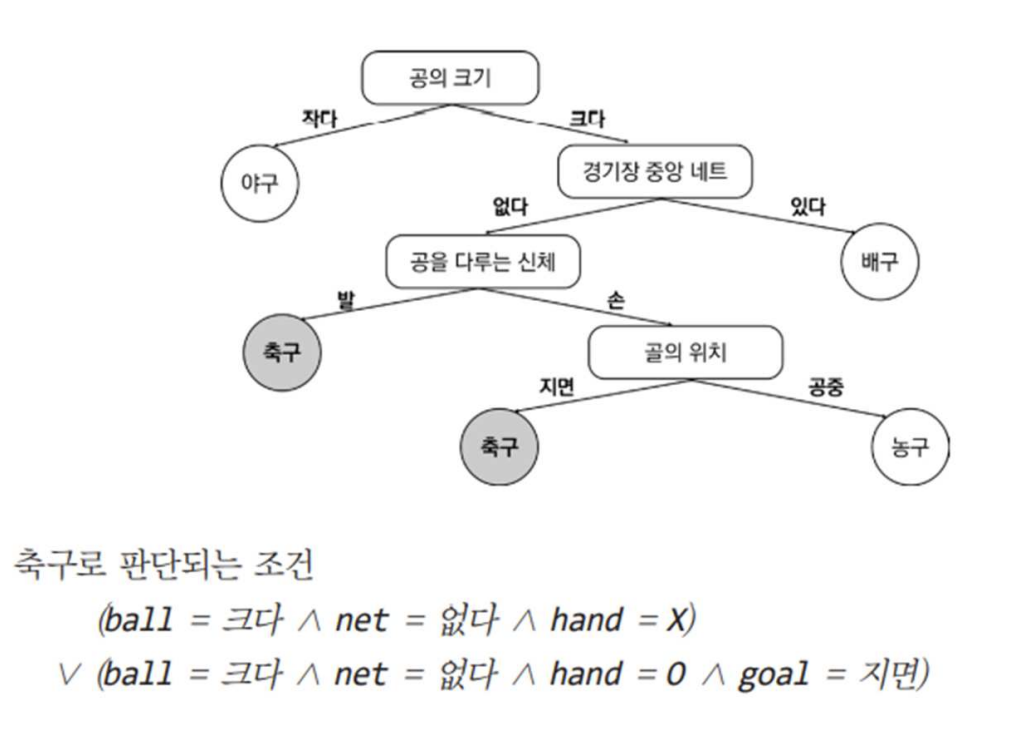
다음 그림을 살펴보겠습니다.
이전 그림과는 다르게 internal node가 살짝 수정되었습니다.
leaf node에 '축구'에 해당하는 클래스가 2개인 것을 확인할 수 있습니다.
이때 어떠한 데이터가 들어왔을 때, 축구로 예측하는 경우는 2가지 임을 알 수 있습니다.
어떤 데이터가 '축구'로 분류되기 위해서는
1. ball이 크고 net는 없어야하며 hand를 써서는 안됩니다.
2. ball이 크고 net는 없어야하고 hand를 쓰는 것이 가능하며 goal은 지면에서 들어가야합니다.
결국 1과 2의 disjunction of conjuntion(논리합)으로 표현할 수 있습니다.
 
 

어떤 속성이 가장 중요한가?

그렇다면 root node와 internal node에 들어갈 속성들은 어떻게 결정할 수 있을까요?
이때 사용하는 개념이 information gain(정보 이득) 입니다.
information gatin은 특정한 속성이 원하는 분류 방식에 부합하게 데이터를 나누는지 측정할 수 있는 척도입니다.
entropy를 이용한 것과 Gini index를 이용한 것이 있는데 우선 entropy를 이용한 것에 대해 먼저 알아보겠습니다.
 
 

Entropy

우선 entropy 공식은 아래와 같습니다.

lg는 밑이 2인 log를 뜻합니다.
 
그럼 p+와 p-에 대해 알아보겠습니다.
만약 특정 데이터 집합이 주어져 있는데 두 부류로 나눌 수 있다고 가정하겠습니다. 한 부류를 양성, 다른 부류를 음성이라고 두면 되는데 전체 데이터 중에 양성(positive)인 클래스의 비율을 'p+', 음성(negative)인 클래스의 비율을 'p-'라고 두면 됩니다.
예를 들어보겠습니다.

그림과 같이 빨간공이 4개, 파란공이 2개인 data set을 생각해 보겠습니다.
빨간공 class를 positive라고 두면, 파란공 class는 자동으로 negative가 됩니다.
 
p+ = 4/6
p- = 2/6
 
이제 entropy 공식의 모든 파라미터 값을 알고 있으므로 공식에 대입해 주어진 data의 entropy를 구할 수 있을 것입니다.

 
하지만 이렇게만 봐서 entropy가 data set에서 어떤 척도로 작용하는지 감을 잡기가 어렵습니다. 조금 더 극단적인 예를 들어보겠습니다.
 

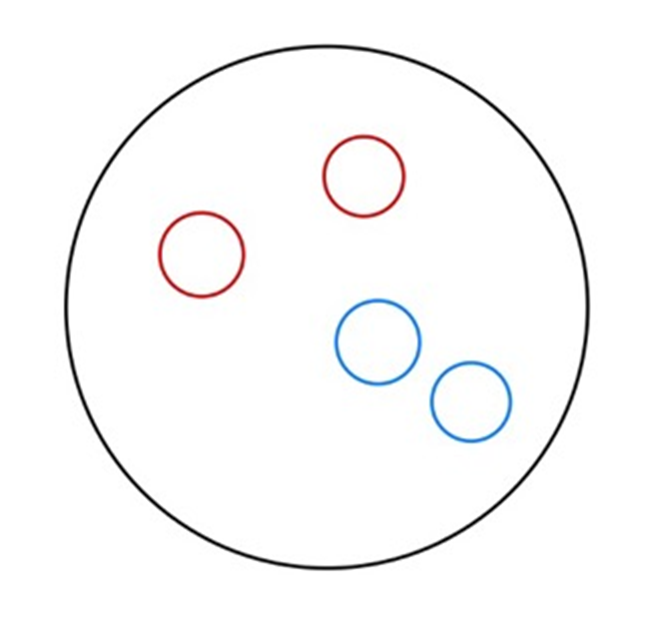
주어진 집합을 보면 빨간공이 2개, 파란공이 2개로 1:1의 비율을 가지고 있는 data set입니다.
p+ = 1/2
p- = 1/2
 
p+와 p-의 값 또한 같습니다.
공식에 대입해 entropy값을 구해보겠습니다.

entropy값이 1이 나왔습니다. 이처럼 하나의 data set에 2개의 class label이 같은 크기로 존재할 때 entropy값이 1이 나오는 것을 확인할 수 있습니다. 이러한 경우를 불순도가 높고 순도가 낮다고 이야기하며 entropy는 일반적으로 불순도의 양을 나타냅니다. 주어진 데이터에서는 entropy값이 1로 아주 높은 상태이므로 불순도가 높다고 이야기할 수 있습니다.
 
또 다른 예를 살펴보겠습니다.

다음 데이터는 빨간공 4개만 존재하는 data set입니다.
p+ = 1
p- = 0
 
마찬가지로 공식에 대입해 entropy값을 계산해보겠습니다.

entropy값이 0이 나오는 것을 알 수 있습니다. entropy는 불순도와 같은 개념이라고 했으므로 그 값이 0이라는 것은 불순도가 낮고 순도가 매우 높은 상태라는 것입니다.
 
만약 data set에 속한 data들이 두 개의 class label로 분류되는 것이 아닌 C라는 class 집합의 각 class로 나눠질 수 있다고 한다면, 그 때의 entropy는 아래와 같이 구합니다.

 
 

그림과 같이 entropy는 data set에서 각 클래스 별로 구성 비율이 비슷할 때 가장 높은 값을 가지는 것을 알 수 있습니다.
 
 

Information gain

Information gain은 정보의 이득입니다. data set에서 특정 속성에 따라 data를 분할 할 때 줄어진 entropy로 정의합니다.
어떤 속성 A가 가지는 모든 값들의 집합을 A라고 할 때, 표본 S를 나누어서 얻는 information gain은 아래와 같습니다.

그림을 그려 시각적으로 확인해보겠습니다.
 

위와 같이 S인 root node와 S1, S2인 leaf node가 존재합니다.
root node에서 특정 속성 A로 나눈 것입니다.
이때 S집합의 entropy를 H(S), S1은 H(S1), S2는 H(S2)라고 둘 수 있습니다.
 
leaf node로 나눠진 두 data set은 S에서 온 것임으로 두 집합의 크기를 합하면 |S|가 됩니다.

전체 크기 |S|에서 각 leaf node마다 얼마만큼의 개수로 나누어 졌는지 각각의 비율을 표현할 수 있습니다.

그렇게 되면 S1집합은 |S1|/|S|의 비율을 가지고
S2집합은 |S2|/|S|의 비율을 가집니다.
 
이때 각각의 비율을 우리는 weight(가중치)로 정의합니다.
그렇게 된다면 leaf node로 분리된 집합에서 각각의 가중치와 entropy를 곱하고 그것을 더함으로써 S집합에서 뻗어나간 leaf node들의 불순도를 생각해볼 수 있습니다. 이때 불순도 값이 최소가 되어야 좋은 것이며 그렇게 되면 information gain의 값은 커지게 됩니다. 식을 보면 아래와 같습니다.

data set이 2개의 부류가 아닌 여러개로 나누어질 수도 있으므로 좀 더 일반적인 공식은 아래와 같습니다.

 
결론적으로 우리는 node에서 A집합에 있는 속성을 고를 때, information gain의 값을 최대로 하는 방향으로 속성을 선택합니다. 이러한 과정을 지속적으로 반복하는 것이 Decision Tree (의사결정나무)입니다.
 
 

지니 불순도

지니 불순도 또한 이득이 되는 특성을 고르기 위한 방식 중 하나 입니다. information gain과 마찬가지로 Decision Tree에서 사용됩니다.
entropy의 개념 자체가 다소 복잡한 수식과 계산을 요구하기 때문에 이를 피하기 위해 지니 불순도는 많이 사용하는 개념입니다.
지니 불순도는 entropy의 대체 척도라고 볼 수 있는데, 하나의 그룹 내에 섞여 있는 n개 종류의 레이블이 있고, 레이블이 i인 객체 비율이 pi라고 할 때 아래와 같은 값을 가집니다.

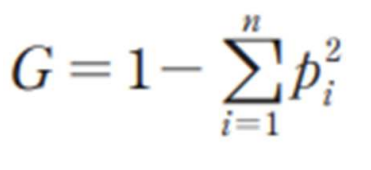
결국 각 비율의 제곱의 합을 계산하고 그 값을 1에서 빼는 방식으로 불순도를 계산하는 것입니다.
 
지니 불순도를 이용하여 결정 트리를 만드는 방법을 CART알고리즘이라고 합니다.
CART는 calssification and regression tree의 약자로 현재 data가 섞여 있는 노드를 두 개의 노드로 나눌 때 어떤 속성과 해당 속성에 어떤 값을 기준으로 쪼갤 것인지를 찾는 알고리즘입니다.
 
쪼개어 얻는 두 node를 L과 R이라고 하고, 각 원소의 개수를 mL, mR이라고 하고 원래 node의 개수를 m이라고 하겠습니다.
이때 각 node 별로 지니 불순도가 결정되는데 entropy와 마찬가지로 weight와 지니 불순도값을 곱해 그것을 최소로 하는 것이 목적입니다. 그 식은 아래와 같습니다.