본 포스팅은 충남대학교 이윤희 교수님의 수리통계및실습 수업과 Probability and Statistical Inference(Hogg, Tanis, Zimmerman 저)를 참고하였습니다.
우리가 고등학교 때 배운 binomial distribution은 다음과 같습니다.
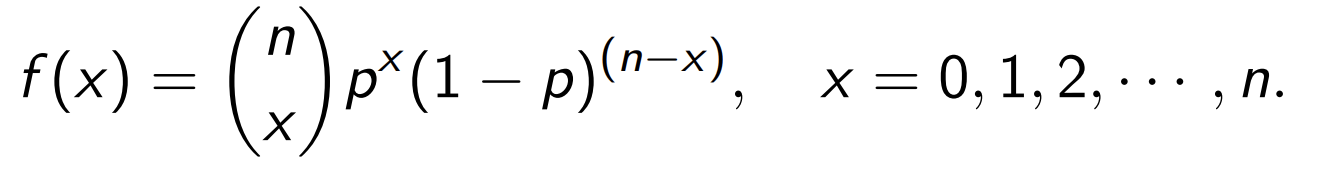
space of X가 discrete한 타입에 대해서
성공할 확률을 p
실패할 확률을 q (= 1-p)라고 했을 때
x번 성공할 확률을 계산하는 방법입니다.
위 식은 그때의 p.m.f.를 나타낸 것입니다.
총 n번의 시행 중 x만큼의 성공을 함으로 C(n, x)를 통해 성공 회차의 index를 결정하고
서로 다른 시행에서 성공과 실패는 independent하기 때문에 위와 같은 식이 나옵니다.
Def) Bernoulli experiment
(1). random experiment를 했을 때 outcome space (sample space)가 성공 혹은 실패로 나오게 된다면 이 experiment를 Bernoulli experiment라고 합니다.
(2). Bernoulli 시행은 서로 independent한 시간에 일어납니다.
요약하면 Bernoulli trial(베르누이 시행)은 서로 독립적인 시간에 일어나야 하며 결과값이 '성공' 혹은 '실패'로 나누어지는 시행을 말합니다.
이제 Bernoulli trial의 random variable에 대해 알아보겠습니다.
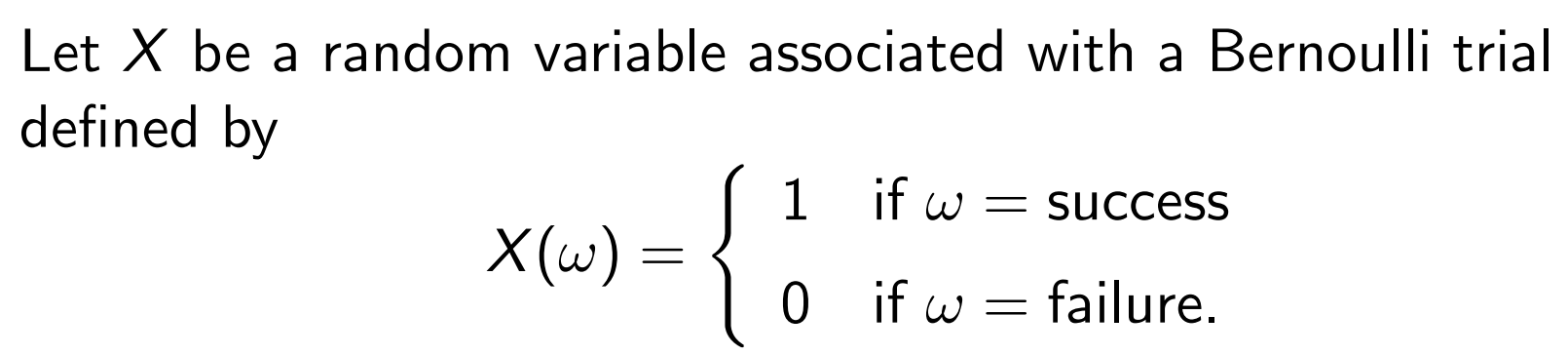
이때의 p.m.f.는 아래와 같습니다.
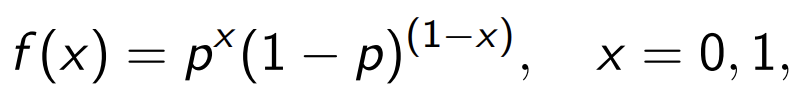
Bernoulli trial은 한 번의 experiment에 대한 것입니다. 그렇기 때문에 실해 혹은 성공의 확률만 존재합니다.
그렇기 때문에 Bernoulli distribution에 대한 p.m.f를 위와 같이 구성할 수 있는 것입니다.
이제 평균과 분산을 구해보겠습니다.
expectation의 정의에 따라 평균을 구할 수 있습니다.
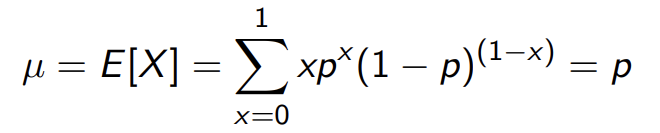
variance도 마찬가지로 expectation을 이용해 계산하면 쉽게 구할 수 있습니다.
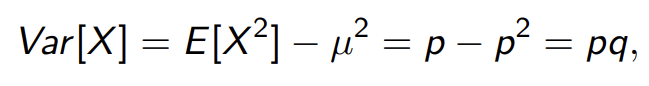
여기서 q = 1 - p입니다.
Binomial distribution

Bernoulli trial에서 Space of X가 1(success) or 0(fail)이었다면 Binomial distribution에서는 success의 횟수입니다.
총 n번의 시행 중 성공할 확률을 계산하는 것입니다.
다르게 말하면 Bernoulli trial을 n번 시행하는 것이라 볼 수 있습니다.
p.m.f.를 자세히 살펴보겠습니다.

n번의 시행 중 x번 success한다고 가정하겠습니다. 그럼 n개의 experiment에서 success할 경우의 수를 계산하면 C(n, x)입니다. 성공할 확률을 p라고 했으므로 p to x이고 1-q는 실패할 확률이므로 (1-p) to (n-x)가 됩니다.
Binomial experiment는 아래 4가지 조건을 만족합니다.

(1). Bernoulli experiment가 n번 시행된 것입니다.
(2). 각 experiment는 independent합니다.
(3). success할 확률을 p, failure할 확률을 q = 1 - p로 계산합니다.
(4). random variable X 즉 Space of X는 n번의 시행 중 success일 횟수입니다.
이러한 Binomial distribution은 X ~ B(n, p)로 표현합니다.
Example

이제 Binomial distribution의 mean과 variance를 각각 구할 수 있습니다.
mean부터 먼저 증명해보겠습니다.

variance또한 간단히 구할 수 있습니다.
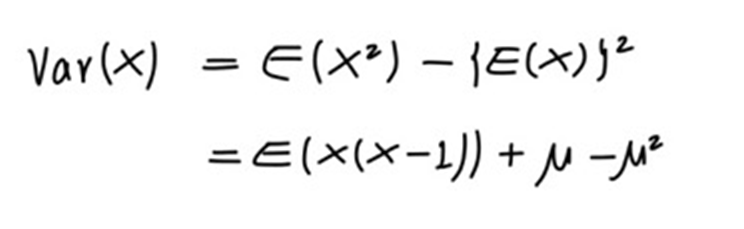
여기서 E[X(X-1)]을 따로 빼서 구해보겠습니다.
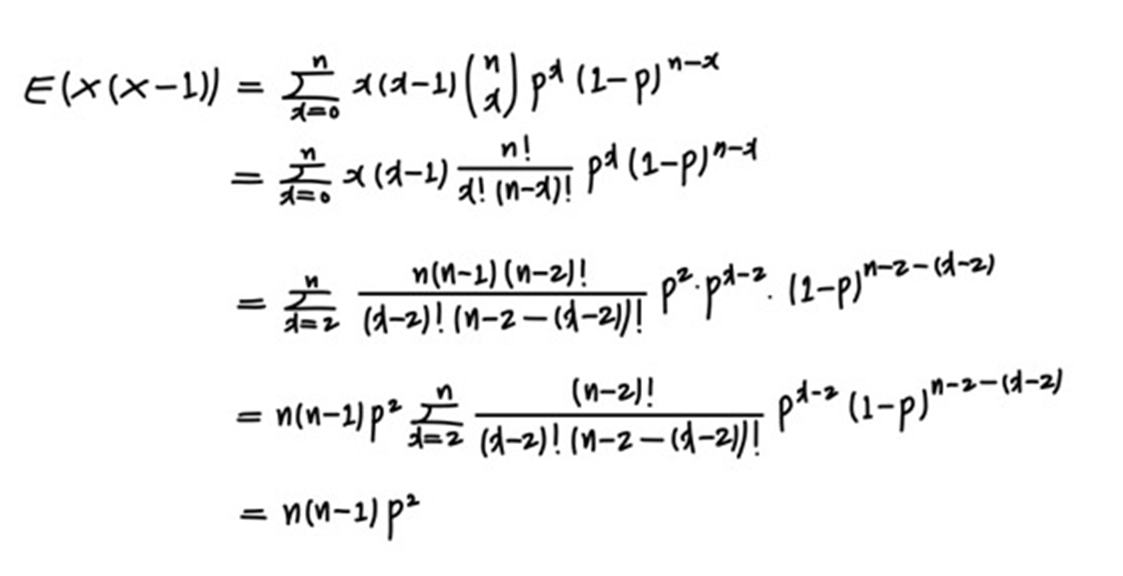
다시 variance로 돌아오면
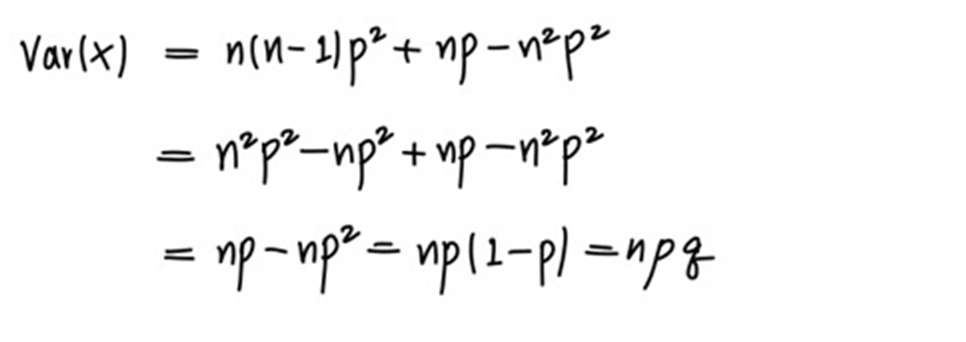
X ~ B(n, p)에서 mean은 np, variance는 npq임을 알 수 있습니다.
'수학과 > 수리통계및실습' 카테고리의 다른 글
| 5. Moment-Generating-Function (모멘트 생성 함수) (0) | 2023.09.19 |
|---|---|
| 4. Mathematical Expectation (0) | 2023.09.18 |
| 3. Random Variables of the Discrete Type (이산 확률변수) (1) | 2023.09.17 |
| 2. Bayes' Theorem (베이즈 정리) (0) | 2023.09.12 |
| 1. Properties of Probability(확률의 성질) (1) (0) | 2023.09.05 |



