본 포스팅은 충남대학교 이윤희 교수님의 수리통계및실습 수업과 Probability and Statistical Inference(Hogg, Tanis, Zimmerman 저)를 참고하였습니다.
Def) 1.1.1. Random Experiments
통계학에서 우리가 시행하는 experiments는 outcome이 어떤지 확실하게 알 수 없습니다. 이때 시행하는 experiments를 random experiments라고 부릅니다. outcome이 어떻게 나올지는 시행 이후 알 수 있는 것입니다. experiment를 시행하기 이전에는 outcome을 알 수 없기 때문에 random이라는 말이 붙습니다.
정확한 outcome을 알 수는 없으나 가능한 outcome에는 어떤 것이 있을지 예측할 수는 있습니다. 가령 dice를 던졌을 때 나올 수 있는 number는 1~6까지의 숫자가 될 수 있는 것입니다.
Def) 1.1.2. Sample Space and Event
(1). 모든 가능한 outcome들의 set을 Sample Space 혹은 Outcome Space라고 부릅니다. 일반적으로 Sample Space라고 많이 불립니다. 우리말로는 표본공간이라고도 불립니다.
(2). Sample Space가 주어졌을 때, Sample Space의 subset이 되는 집합을 A라고 하면, A를 Event라고 부릅니다. Event Set은 반드시 Sample Space의 subset이 됩니다.
(3). random experiments를 시행했을 때 A(Event Set)이 outcome으로 나온다면 A is occurred 라고 이야기합니다.
dice를 다시 예로 들면 Same Space는 {1, 2, 3, 4, 5 ,6}이고 Event는 {5, 6}이라고 하겠습니다. Experiments의 outcome이 6이 나오면 Event가 발생한 것입니다.
Def) 1.1.3. Algebra of sets
위 정의들을 살펴봤을 때, 일반적으로 우리가 알고있는 set과 위에서 공부한 event는 서로 닮은점이 많습니다. Sample Space와 Event가 Set과 닮아있는 점들이 많으므로 Algebra of sets의 defintion을 살펴보겠습니다.
(1). ∅ 은 null 혹은 empty set(공집합)이라고 부릅니다.
(2). A ⊆ B 에서 A는 B의 subset이라고 부릅니다.
(3). A ∪ B 는 A와 B의 union이라고 부릅니다.
(4). A ∩ B 는 A와 B의 intersection이라고 부릅니다.
Def) 1.1.4. Mutually exclusive and exhaustive events
(3). (1)과 (2)를 condition을 모두 만족한다면 mutually exclusive and exhaustive events라고 이야기 합니다.
그림으로 보면 아래와 같습니다.
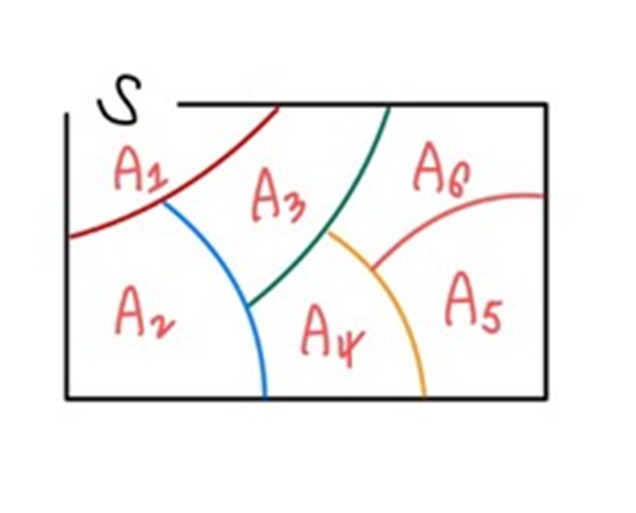
위 그림은 mutally exclusive and exhaustive event 인 집합입니다. Set Theory에서 등장하는 equivalence relation의 partition과 같은 그림입니다.
그 외에도 집합에는 Commutative Laws(교환법칙), Associative Laws(결합법칙), Distributive Laws(분배법칙), De Morgans's Laws(드모르간법칙)이 성립합니다.
교환, 결합, 분배, 드모르간법칙들은 벤다이어그램으로 모두 증명이 가능합니다.
Def) 1.1.5. Probability
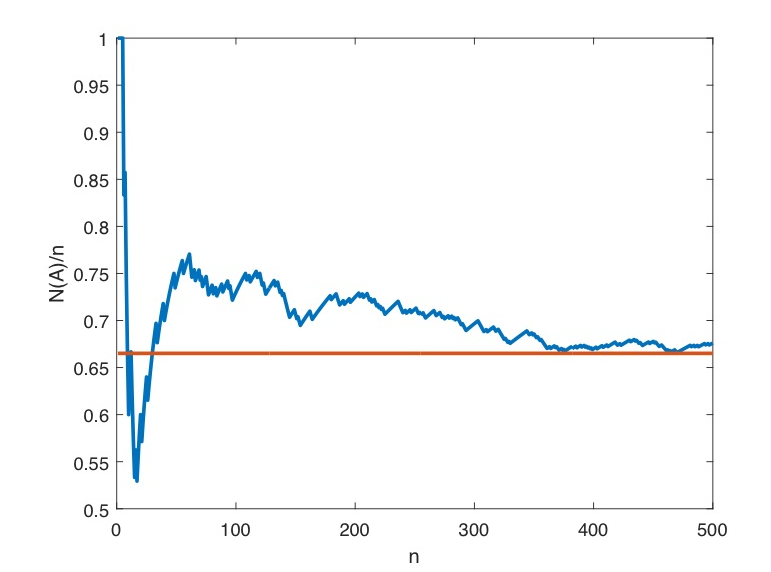
probability를 정의하기 위해서는 우선 experiment 시행 횟수를 늘려야합니다. 그렇게 해서 A(event)가 발생하는 number를 count하고(countable set에 대해서) 그때 시행된 A의 개수를 N(A)라고 합니다. N(A)/n을 relative frequency(상대도수)라고 부르며 n값이 (experiment 횟수)가 증가할 수록 상대도수 값은 stable해 집니다.
그렇게 stable 해진 값이 p라는 값에 가까워질 때 p를 event A의 probability라고 부르고 P(A)라고 표현합니다.
Example
6개의 눈이 있는 fair한 주사위가 있다고 합시다. 주사위를 총 6번 던지는데 만약 k번째 시행에 눈의 수가 k가 나온다면 그때를 match라고 부릅니다. 6번의 시행 중 한 번이라도 match가 된 경우를 success로 하고 6번의 시행 중 한 번도 match가 되지 않은 경우를 failure로 하겠습니다. event A를 success로 했을 때 P(A)를 구하는 것이 문제입니다.
sol)

그림으로 보면 아래와 같습니다.
'수학과 > 수리통계및실습' 카테고리의 다른 글
| 6. The Binomial Distribution (이항 분포) (0) | 2023.09.26 |
|---|---|
| 5. Moment-Generating-Function (모멘트 생성 함수) (0) | 2023.09.19 |
| 4. Mathematical Expectation (0) | 2023.09.18 |
| 3. Random Variables of the Discrete Type (이산 확률변수) (1) | 2023.09.17 |
| 2. Bayes' Theorem (베이즈 정리) (0) | 2023.09.12 |



